
Papadopoulos A (2015) The half-normal specification for the two-tier stochastic frontier model. Owen D (1956) Tables for computing bivariate normal probabilities. Meeusen W, van den Broeck J (1977) Efficiency estimation from Cobb–Douglas production functions with composed error.
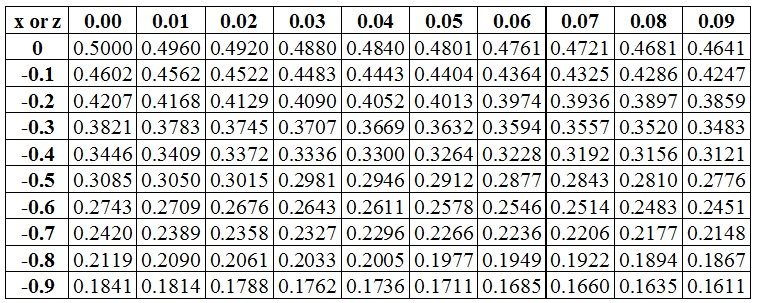
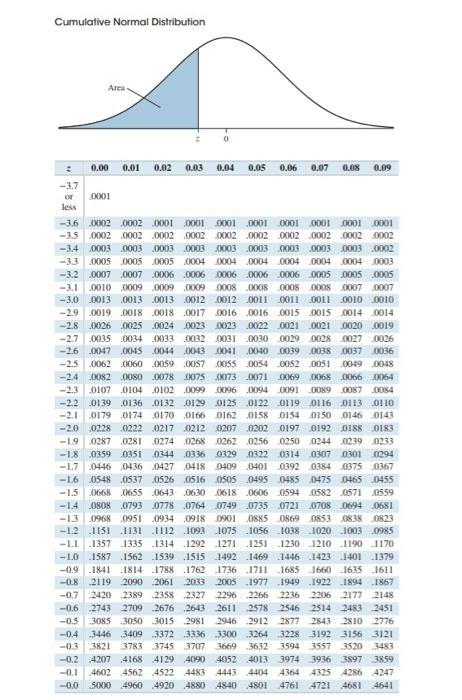
Mee RW, Owen D (1983) A simple approximation for bivariate normal probabilities. Loperfido N (2002) Statistical implications of selectively reported inferential results. Gupta AK, Chen T (2001) Goodess-of-fit tests for the skew normal distribution. Gradshteyn IS, Ryzhik IM (2007) Tables of integrals, series and functions, vol 7. Genz A, Bretz F (2009) Computation of multivariate normal and t probabilities. Genz A (2004) Numerical computation of rectangular bivariate and trivariate normal and t probabilities. Commun Stat Theory Methods 36(9):1705–1717ĭrezner Z, Wesolowsky GO (1989) On the computation of the bivariate normal integral. Metron 68(3):299–308Ĭhang SM, Genton M (2007) Extreme value distributions for the skew-symmetric family of distributions. Cambridge University Press, CambridgeĬapitanio A (2010) On the approximation of the tail probability of the scalar skew normal distribution. Scand J Stat 12(2):171–178Īzzalini A, Capitanio A (2014) The skew-normal and related families. J Adv Res 1(4):341–350Īzzalini A (1985) A class of distributions which includes the normal ones. J Product Anal 52:29–35Īshour S, Abdel-hameed MA (2010) Approximate skew normal distribution. J Econom 6:21–37Īmsler C, Schmidt P, Tsay WJ (2019) Evaluating the CDF of the distribution of the stochastic frontier composed error. By a simulated example, we show that the use of approximations instead of the theoretical exact expressions may be critical in obtaining meaningful and valid estimation results.Īigner DJ, Lovell CAK, Schmidt P (1977) Formulation and estimation of stochastic frontier production function models. We find that the expressions based on the bivariate Normal distribution are quite accurate in the central portion of the distribution, and we propose several new approximations that are accurate in the extreme tails. We investigate the accuracy of the evaluation of the cdf using expressions based on the bivariate Normal distribution, and also using simulation methods and some approximations. The cdf must be evaluated in models in which the composed error is linked to other errors using a Copula, in some methods of goodness of fit testing, or in the likelihood of models with sample selection bias. This distribution arises in the stochastic frontier model because it is the distribution of the composed error, which is the sum (or difference) of a Normal and a Half-Normal random variable. In this paper, we consider various methods for evaluating the cdf of the Skew Normal distribution.


 0 kommentar(er)
0 kommentar(er)
